Nối tiếp bài review tiểu thuyết 2 số phận được đăng tải khá lâu trước đây trên Share Ngay được khá nhiều anh em ủng hộ, bài hôm nay không phải mình viết mà là thằng bạn mình. Cơ bản là lâu rồi Share Ngay không có bài dịch mới và nó cũng muốn đóng góp 1 phần cho Share Ngay.
Đợt này nó khá bận nên sẽ không dịch được, thay vào đó nó sẽ chia sẻ 1 vài mẫu chuyện thú vị trong tựa sách đang đọc, khá là hay mang tên: How Not to Be Wrong: The Power of Mathematical Thinking của tác giả Jordan Ellenberg.

480 trang trên cuốn sách cho người đọc rất nhiều cảm xúc, có chút hài hước nữa. Quyển sách dường như làm mới suy nghĩ và tư duy khi kết hợp rất nhiều kiến thức về hình học, lịch sử quân sự, khoa học máy tính, chính trị, thống kê, cờ bạc, y học, đạo đức và triết học.
Cuốn sách về toán học nhưng không hề khô khan 1 chút nào
Thực sự đây là 1 cuốn sách phong phú, phong phú bởi kiến thức của tác giả và những biện chứng vô cùng sâu sắc, và tin minh đi – nó vô cùng chặt chẽ và đầy đủ.

Đọc xong bạn sẽ hiểu xác suất, thống kê quan trọng như thế nào trong cuộc sống hiện đại. Nói thật trên 50% bạn đọc bài này, mình nghĩ rằng các bạn đã quên mất: để đạt được dự đoán tốt trong bộ môn xác suất thống kê, chúng ta cần 1 tập dữ liệu khổng lồ, sai và loại sai liên tục. Áp dụng vào cuộc sống, bạn sẽ thấy mọi thứ ngẫu nhiên dường như không đoán trước được, nhưng tệp dữ liệu bạn đang sống cho phép bạn dự đoán nhiều thứ hơn ảnh hưởng trực tiếp đến bạn thay vì mơ hồ tìm kiếm những thứ phi xác định.
Nếu có ai hỏi bạn Lộc rằng bạn đọc quyển này chưa?
Xin thưa, Lộc chưa đọc nhưng Lộc chém rất mát tay. Đừng như Lộc.
Sau đây là nội dung bài viết của thím Cò:
Chào các bạn, đây là lần đầu mình viết review sách, nếu lủng củng và không hay, thì các bạn bỏ qua cho.
Mình sẽ mở ra 2 câu chuyện thú vị mà mình đọc trong quyển sách này, thực ra mình sẽ chỉ nói sơ qua về toán học thông qua 1 biểu đồ, những phép toán,… để tìm hiểu sâu các bạn nên đọc qua quyển sách trên.
Câu chuyện biểu đồ Bell Curve và đạo Trung dung:
Như các bạn đã biết thì châu Á chúng ta có đạo Trung dung từ rất lâu rồi, mà mấy ông nghĩ ra đạo đó chắc chả giỏi toán cho lắm. Lạ cái là mãi đến gần đây mới có 1 quyển sách ở trời Tây viết về đạo này dưới mô hình toán học với 1 thái độ hết sức cẩn trọng. (mình cũng không chắc, biết đâu họ biết lâu rồi nhưng mình chưa biết).
Để hiểu đạo Trung dung là gì nào thì các bạn xem qua biểu đồ Bell Curve dưới đây, mình sẽ giải thích 1 chút cho mọi người hiểu:
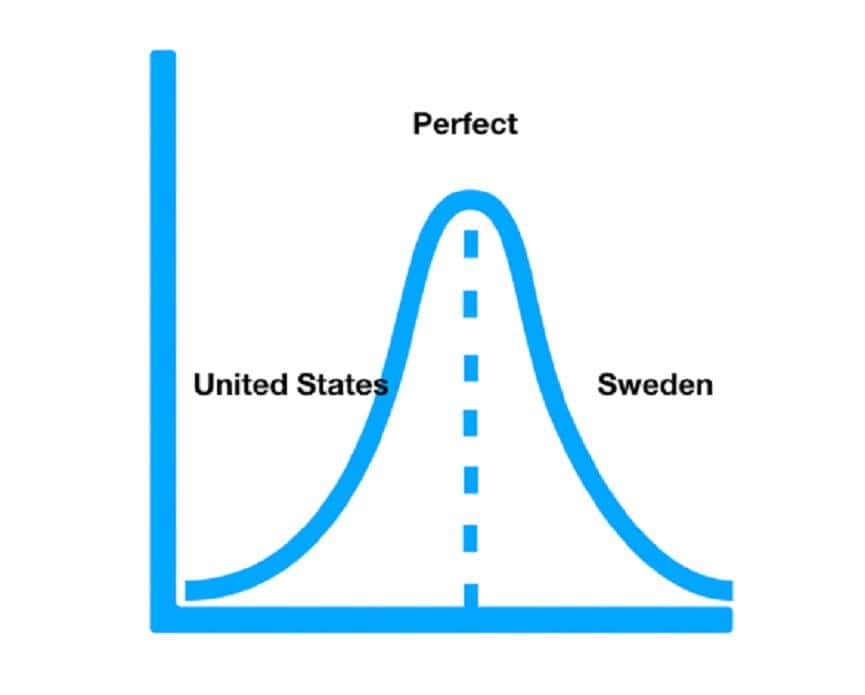
“Cái gì quá cũng không tốt” hay nói đúng hơn “cân bằng” chính là từ đại diện cho bell curve bên trên và đại diện cho từ “trung dung”. Biểu đồ này được đề cập trong cuốn “How Not To Be Wrong” của “Jordan Ellenberg”, một cuốn toán học ứng dụng cực hay nhưng éo nổi lắm. Tuy nhiên phàm là cái gì không nổi mà thú vị, mình lại muốn nhiều người biết và hôm nay mình muốn giới thiệu em nó tới các bạn. Mình mới đọc 1/3 thôi nhưng thấy hay quá nên muốn share liền.
Vậy tác giả đang muốn nhắn nhủ gì thông qua biểu đồ này?
Đơn giản thôi. Nước Mỹ thì muốn như Thụy Điển, còn Thụy Điển thì đang muốn như nước Mỹ. Nhưng đấy chỉ là ý nghĩ trong thời xưa xưa, còn giờ thì họ nhận ra “cái gì quá cũng không tốt”, vì vậy điểm chính giữa chính là điểm hoàn hảo mà ai cũng hướng đến
=>>> một đất nước dân không lo nghèo đói, không tồn tại sự đố kỵ ghen ghét nhưng vẫn có 1 sự kích thích vừa đủ để người ta chăm chỉ làm việc 1 cách thoải mái vui vẻ, không ỷ lại.
Chính ra thì ở đời, người ta chỉ thực hiện được “cái gì quá cũng không tốt” chứ hiếm có ai đạt được điểm “cân bằng hoàn hảo” cả về thể trạng lẫn tinh thần. Có lẽ chỉ có đức Gautama và các vị La Hán (theo những gì chúng ta biết) là đạt được điều này.
Nói đến đây các bạn nên đọc qua bài viết:
… để hiểu sâu hơn cái gọi là niết bàn (trạng thái cao nhất của giác ngộ) – nơi mọi thứ đạt được ở điểm “cân bằng hoàn hảo”.
Câu chuyện về nhà toán học trong chiến tranh:
Tiếp đến 1 câu truyện thứ 2 cũng thú vị không kém nói về 1 nhà toán học trong thế chiến. Công việc hàng ngày của ông này cùng hàng trăm nhà toán học khác là chỉ ngồi 1 chỗ trong phòng để tính toán làm sao thả bom đúng chỗ, làm sao để build 1 cái máy bay ổn,.. và xây dựng giáp cho xe tăng và máy bay, etc..

Ví dụ 1 cái máy bay chiến đấu thì mình nên đắp thêm sắt vô chỗ nào trên thân máy bay để nó vừa bay tốt vừa đỡ bị bắn thủng. Vì nếu đắp nhiều quá thì máy bay nặng nề không cơ động, còn ít quá thì dễ bị bắn hạ.
=> nên là bao nhiêu và đắp chỗ nào là đủ. Ông sĩ quan đến hỏi nhà toán học, để tính toán dựa trên data thu thập được của 1 đống máy bay đã bị bắn, từ đó đưa cho bên sản xuất và lắp ráp.

Trông thế thôi chứ 1 cuộc chiến mà có mưu kế siêu việt của Nguyễn Chích hay 1 trận highlight Tốt Động – Chúc Động là hiếm khi xảy ra trên chiến trường. Cái thường diễn ra là 2 bên chạy đua vũ trang, tối đa hóa mọi quy trình chiến tranh, ai hơn tầm 5% là bên đó thắng rồi. Giả sử bên A hơn 5%/ ngày trong trận chiến kéo dài 3 tháng là bên B tổn thất “HƠN” 5%*90 ngày là vỡ mồm rồi (ý hiểu của mình, sai thì thông cảm nha).
Thực ra khi search Google về cuốn sách này để anh em có chỗ mua thì mình đọc 1 bài chi tiết hơn rất nhiều về phần 2 này, các bạn nên đọc qua vì nó hay nhé (cảm giác viết xong mà có người viết hay hơn thiệt đau khổ, nhưng vì a/e mình phải giới thiệu).
Tựu chung lại thì tác giả muốn nói rằng, toán học cũng chỉ là công cụ thôi, phần còn lại vẫn là tư duy critical, common sense của mỗi chúng ta. Chúng ta nhìn bài toán thi học sinh giỏi khô khan, khó giải nhưng không hề biết giải xong rồi để làm gì. Còn cái ông bên trên ổng nghĩ ra bài toán để xem là lắp ráp máy báy như thế nào cho đỡ bị bắn rụng. Cái tư duy của ổng mới là chuẩn, mới là chủ động.
Cuối cùng, các bạn có thể xem video tác giả chém gió về quyển sách của mình tại đây:
Link mua sách:
- Amazon: How Not to Be Wrong: The Power of Mathematical Thinking
- Có link tiki nhưng nhọ cái là nó ngừng bán cmnr.
Cuối cùng, mình cảm ơn thím Cò đã dành thời gian để chia sẻ những kiến thức mình có được trong quá trình đọc sách. Hi vọng là bạn sẽ chia sẻ nhiều hơn nữa trong tương lai, mình tin rằng người đọc sẽ thích bởi vì chia sẻ là hạnh phúc mà. Hehe.










sách này có bản tiếng việt không ạ??
Không có bạn à.
thanks bạn nhiều
Yeah, mình không thấy comment nên rep hơi chậm. Chúc bạn ngày đầu tuần vui vẻ nhé.
lấy link này qua “Nhận get ebook free 100% từ Amazon” đc ko ad ới :v
Mình không hiểu lắm. :v
Bài dịch hay mà hơi ít ad…^^
Cảm ơn bạn, Việt Anh mới đọc 1/3 quyển sách và bạn thấy có 2 câu chuyện vui vui nên share a/e ý.
Xin thưa, Lộc chưa đọc nhưng Lộc chém rất mát tay. Đừng như Lộc.
^^
Các bạn chém Lộc ko trượt phát nào. :v